assert get_number_of_gate_params(ql.HGate) == 0
assert get_number_of_gate_params(ql.CXGate) == 0
assert get_number_of_gate_params(ql.U1Gate) == 1
assert get_number_of_gate_params(ql.U2Gate) == 2
assert get_number_of_gate_params(ql.U3Gate) == 3Qiskit circuits backend
Qiskit based quantum circuit backend.
Utils
get_number_of_gate_params
get_number_of_gate_params (gate_cls:type[qiskit.circuit.gate.Gate])
instruction_name_to_qiskit_gate
instruction_name_to_qiskit_gate (name:str)
get_target_control_qubits
get_target_control_qubits (qc:qiskit.circuit.quantumcircuit.QuantumCircu it, gate:qiskit.circuit.gate.Gate)
Get the target and control qubits of a Qiskit Gate of a QuantumCircuit.
Backend
CircuitsQiskitBackend
CircuitsQiskitBackend ()
Backends implement at least these functions.
Test
from genQC.platform.tokenizer.circuits_tokenizer import CircuitTokenizergenqc <-> backend
tensor = torch.tensor([
[3, 0, -2, 0, 0],
[0, 0, 2, 0, 1],
[0, 3, -2, 3, 0],
], dtype=torch.int32)
params_tensor = torch.tensor([ # ... [max_params, time]
[0, 0, 0, 0, 0.9],
[0, 0, 0, 0, -0.7]
])
vocabulary = {"u2":1, "ccx":2, "h":3}
tokenizer = CircuitTokenizer(vocabulary)
instructions = tokenizer.decode(tensor, params_tensor)
instructions.print()CircuitInstruction(name='h', control_nodes=[], target_nodes=[0], params=[6.2831854820251465, 6.2831854820251465])
CircuitInstruction(name='h', control_nodes=[], target_nodes=[2], params=[6.2831854820251465, 6.2831854820251465])
CircuitInstruction(name='ccx', control_nodes=[0, 2], target_nodes=[1], params=[6.2831854820251465, 6.2831854820251465])
CircuitInstruction(name='h', control_nodes=[], target_nodes=[2], params=[6.2831854820251465, 6.2831854820251465])
CircuitInstruction(name='u2', control_nodes=[], target_nodes=[1], params=[11.9380521774292, 1.8849557638168335])backend = CircuitsQiskitBackend()
qc = backend.genqc_to_backend(instructions)
qc.draw("mpl")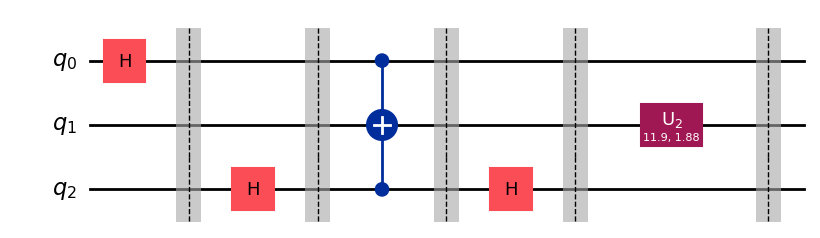
dec_instructions = backend.backend_to_genqc(qc)
dec_instructions.print()CircuitInstruction(name='h', control_nodes=[], target_nodes=[0], params=[])
CircuitInstruction(name='h', control_nodes=[], target_nodes=[2], params=[])
CircuitInstruction(name='ccx', control_nodes=[0, 2], target_nodes=[1], params=[])
CircuitInstruction(name='h', control_nodes=[], target_nodes=[2], params=[])
CircuitInstruction(name='u2', control_nodes=[], target_nodes=[1], params=[11.9380521774292, 1.8849557638168335])enc_tensor, enc_params_tensor = tokenizer.encode(dec_instructions)
enc_tensor, enc_params_tensor(tensor([[ 3, 0, -2, 0, 0],
[ 0, 0, 2, 0, 1],
[ 0, 3, -2, 3, 0]], dtype=torch.int32),
tensor([[ 0.0000, 0.0000, 0.0000, 0.0000, 0.9000],
[ 0.0000, 0.0000, 0.0000, 0.0000, -0.7000]]))assert torch.allclose(tensor, enc_tensor)
assert torch.allclose(params_tensor, enc_params_tensor)Calculate unitary and optimize circuit
gate_pool = ["u3", "cx", "h"]
qc = backend.rnd_circuit(2, 10, gate_pool, np.random.default_rng())
U_initial = backend.get_unitary(qc)
qc_opt = backend.optimize_circuit(qc, gate_pool, silent=0)
U_opt = backend.get_unitary(qc_opt, remove_global_phase=False)
print(np.round(U_initial, 2))
assert np.allclose(U_initial, U_opt)[[ 0.64+0.59j -0.25+0.04j -0.31-0.27j 0.12-0.02j]
[-0.18-0.18j -0.86+0.11j 0.09+0.08j 0.41-0.06j]
[-0.11+0.05j -0.11+0.4j -0.23+0.1j -0.21+0.84j]
[ 0.37-0.17j -0.03+0.12j 0.78-0.39j -0.05+0.25j]]res = %timeit -o -q backend.get_unitary(qc)
print(f"Timeit get_unitary: {str(res)}")Timeit get_unitary: 524 μs ± 407 ns per loop (mean ± std. dev. of 7 runs, 1,000 loops each)print(f"Initial number of gates {len(qc.data)}:")
display(qc.draw("mpl"))
print(f"After optimization {len(qc_opt.data)}:")
display(qc_opt.draw("mpl"))Initial number of gates 10:
After optimization 3: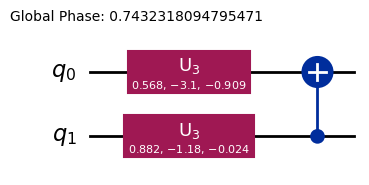
qc_rand = backend.randomize_params(qc_opt, np.random.default_rng())
display(qc_rand.draw("mpl"))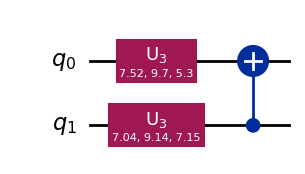
Schmidt-rank-vector
def plot_srv_stat(num_of_qubits, min_gates, max_gates, gate_pool, samples, rng=np.random.default_rng()):
srv_list = list()
for i in range(samples):
qc = backend.rnd_circuit(num_of_qubits, rng.integers(min_gates, max_gates+1), gate_pool, rng)
qc = backend.optimize_circuit(qc, gate_pool)
srv = backend.schmidt_rank_vector(qc)
srv_list.append(srv)
srv_unique, srv_cnt = np.unique(np.array(srv_list), axis=0, return_counts=True)
srv_unique = [f"{s}" for s in srv_unique]
plt.bar(srv_unique, srv_cnt)
plt.title("Different SRV distribution")
plt.show()gate_pool = [ql.HGate, ql.CXGate]
plot_srv_stat(num_of_qubits=3, min_gates=6, max_gates=8, gate_pool=gate_pool, samples=int(1e3), rng=np.random.default_rng())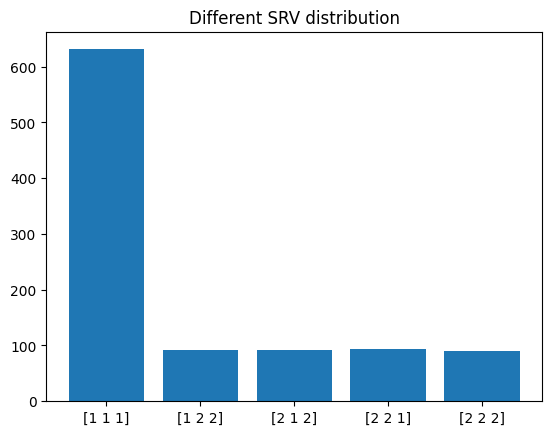
def test_srv(system_dims, init, target):
vec = qi.Statevector(init, dims=system_dims)
vec *= 1/np.sqrt(vec.trace())
srv = backend.schmidt_rank_vector(densityMatrix=qi.DensityMatrix(vec))
assert srv == target, f"srv: {srv}"
print(f"passed test, svr: {srv}")
display(vec.draw('latex', prefix='|\\psi\\rangle = '))#---------------- |0+> = |00>+|01>
system_dims = (2,2)
init = np.zeros(np.prod(system_dims), dtype=complex)
init[0] = 1
init[1] = 1
test_srv(system_dims, init, [1, 1])
#----------------Bell, |00>+|11>
system_dims = (2,2)
init = np.zeros(np.prod(system_dims), dtype=complex)
init[0] = 1
init[3] = 1
test_srv(system_dims, init, [2, 2])
#----------------GHZ, |000>+|111>
system_dims = (2,2,2)
init = np.zeros(np.prod(system_dims), dtype=complex)
init[0] = 1
init[7] = 1
test_srv(system_dims, init, [2,2,2])
#----------------Sym, |000>+|111>+|222>
system_dims = (3,3,3)
init = np.zeros(np.prod(system_dims), dtype=complex)
init[0] = 1
init[13] = 1
init[26] = 1
test_srv(system_dims, init, [3,3,3])
#----------------Wikipedia example, |000>+|101>+|210>+|311>
system_dims = (4,4,4)
init = np.zeros(np.prod(system_dims), dtype=complex)
init[0] = 1
init[17] = 1
init[36] = 1
init[53] = 1
test_srv(system_dims, init, [2, 2, 4])passed test, svr: [1, 1]\[|\psi\rangle = \frac{\sqrt{2}}{2} |00\rangle+\frac{\sqrt{2}}{2} |01\rangle\]
passed test, svr: [2, 2]\[|\psi\rangle = \frac{\sqrt{2}}{2} |00\rangle+\frac{\sqrt{2}}{2} |11\rangle\]
passed test, svr: [2, 2, 2]\[|\psi\rangle = \frac{\sqrt{2}}{2} |000\rangle+\frac{\sqrt{2}}{2} |111\rangle\]
passed test, svr: [3, 3, 3]$$\[\begin{align} |\psi\rangle = \begin{bmatrix} \frac{\sqrt{3}}{3} & 0 & 0 & 0 & \cdots & 0 & 0 & \frac{\sqrt{3}}{3} \\ \end{bmatrix} \\ \text{dims=(3, 3, 3)} \end{align}\]$$
passed test, svr: [2, 2, 4]$$\[\begin{align} |\psi\rangle = \begin{bmatrix} \frac{1}{2} & 0 & 0 & 0 & \cdots & 0 & 0 & 0 \\ \end{bmatrix} \\ \text{dims=(4, 4, 4)} \end{align}\]$$